PA1
01-02:Structure of a Compiler
https://stackoverflow.com/questions/2135788/what-do-c-and-assembler-actually-compile-to
1.Lexical Analysis
Recognize words:Blank/Punctuation/Capital letter
Example: ist his ase nte nce -> is this a sentence
Lexical analysis divides program text into “words” or “tokens”
Example: if x == y then z = 1;else z = 2;
keywords、variable names、constants、operators
Once words are understood,the next step is to understand sentence structure
2.Parsing == Diagramming Sentences --> tree
Actual work: Group words together into higher level constructs
Understand sentence structure --> Understand “meaning”
3.Semantic Analysis
Compiler perform limited semantic analysis to catch inconsistencies
Programming languages define strict rules to avoid such ambiguities
Compilers perform many semantic checks besides variable bindings
4.Optimization
Optimization has no strong counterpart in English
Automatically modify programs so that they can run faster or use less memory
Example: X = Y * 0 is the same as X = 0
valid for integers and invalid for FP(NaN * 0 = NaN)
5.Code Generation
Produces assembly code
A translation into another language
The overall structure of almost every compiler adheres to our outline
Optimization phase is very large in all modern compilers
The proportions have changed since FORTRAN
01-03:The Economy of Programming Language
Application domains have distinctive/conflicting needs.
Programmer training is the dominant cost for a programming language.
New languages tend to look like old languages.
https://www.geeksforgeeks.org/difference-between-assembly-language-and-high-level-language/
01-04:COOL Overview
COOL:Classroom Object Oriented Language
Modern implementation:
Abstraction/Static typing/Reuse(inheritance)/Memory management…
5 programming assignments(PAs)
- Write a COOL program
- Lexical analysis
- Parsing
- Semantic analysis
- Code generation
- optimization(optional)
class Main{
i : IO <- new IO;
//initialize to a new IO object
main():IO{ i.out_string("Hello world!\n") };
//main():Object{ (new IO).out_string("Hello world!\n") };
};
class Main inherits IO{
main():Object { self.out_string("Hello world!\n") };
}
self: name of the current object when the main method runs
(In other languages self is called this)
02-02:Cool Example II
fact(i : Int) : Int {
let fact: Int <- 1 in {
while (not (i = 0)) loop
{
fact <- fact * i;
i <- i - 1;
}
pool;
fact;
}
};
02-03: Cool Example III
class List{
item: Objects;
next:List;
init(i: Object,n: List) : List{
item <- i;
next <- n;
self;
}
flatten() : String {
let string: String <-
case item of
i: Int => i2a(i);
s: String => s;
o: Object => { abort(); "";}
esac;
in
if(isvoid next) then
string
else
string.concat(next.flatten())
fi
};
};
03-01: Lexical Analysis Part 1
lexical analysis(词法分析)
关于lexical analysis中的token
Tokens are defined often by regular expressions, which are understood by a lexical analyzer generator such as lex. The lexical analyzer (generated automatically by a tool like lex, or hand-crafted) reads in a stream of characters, identifies the lexemes in the stream, and categorizes them into tokens. This is termed tokenizing.
categories:identifier/keyword/integer/whitespace/operator/seperator
- Identifier(标识符):以字母开头、由字母或数字组合的字符串
- Integer(整数):一个或一串数字
- Keyword(关键字):又称为预留字(reserved word)
- Whitespace(留白处):空白(blank)、换行(newline)、tab
lexical analysis需要根据规定来对子字符串(substrings)进行归类,向parser传递token
token = <class ,string>
03-02:Lexical Analysis Examples
1.The goal is to partition the string.This is implemented by reading left-to-right,recognizing one token at a time.
2.“Lookahead" may be required to decide where one token ends and the next token begins
PL/I Programming Language One PL/I keywords are not reserved
由于PL/I不预留关键字,在分析词法时面临着巨大挑战
IF ELSE THEN THEN = ELSE;ELSE ELSE = THEN
K V K V V K V V
所以有时需要Lookahead,根据后面内容来进行判断
词法分析目的:
- Partition the input string into lexemes
- ldentify the token of each lexeme
03-03: Regular Languages Part 1
Lexical structure = token classes
We must say what set of strings is in a token class
一Use regular languages
https://en.wikipedia.org/wiki/Regular_expression
two base regular expressions(基本正则表达式):
- regular language
- epsilon(空字符)
three compound regular expressions(复合正则表达式):
-
Union(合并)
Union of the sets of strings
A + B = {a|a∈A} ∪ {b|b∈B} -
Concatenation(连结)
AB = {ab|a∈A ∧ b∈B} -
Iteration
A* = ∪Aⁿ n≥0 //A concatenates with itself By n timesSo the empty string is always an element of a star
The regular expressions over ∑ are the smallest set of expressions including
∑ = {0,1}
1* = "" + 1 + 11 + 111 + ... = all strings of 1's
(1+0)1 = {ab|a∈1+0 ∧ b∈1} = {11,01}
0* + 1* = {0ⁿ|n≥0} ∪ {1ⁿ|n≥0}
(0 + 1)* = "" + (0+1) + (0+1)(0+1) + ... = ∑*
03-03: Regular Languages Part 2
对03-02的总结
Regular expressions specify regular languages
Five constructs
- Two base cases: empty and 1-character strings
- Three compound expressions: union, concatenation, iteration
03-04: Formal Languages
Def. Let ∑ be a set of characters (an alphabet).
A language over ∑ is a set of strings of characters drawn from ∑.
Alphabet = ASCII Language = C programs
L:exp -> set of Strings
把compound expressions分解为几种基本的expressions,然后compute
Why use a meaning function?
-
Makes clear what is syntax, what is semantics
-
Allows us to consider notation as a separate issue
-
Because expressions and meanings are not 1-1
举例,阿拉伯数字和罗马数字两种方式都能表示数字,但在基础计算上罗马数字更为困难,这也表明notation对于理解和计算的重要性
Meaning is many to one!
03-05: Lexical Specifications
Integer:
digit = '0' + '1' + '2' + '3' + '4' + '5' + '6' + '7' + '8' + '9'
因为整数是非空的数字字符串,所以可以用这样的正则表达式来表示
digitdigit* // equal to digit⁺ 用windows自带的charmap
Identifier:
letter = [a-zA-Z]
letter(letter + string)*
Whitespace:
' ' + '\n' + '\t' //blank , newline , tab
(' ' + '\n' + '\t')⁺
以邮箱格式举例
anyone@cs.stanford.edu
letter⁺'@'letter⁺'.'letter⁺'.'letter⁺
以数字类型举例
digit = '0' + '1' + '2' + '3' + '4' + '5' + '6' + '7' + '8' + '9'
digits = digit⁺
opt_fraction = ('.'digits) + ε = ('.'digits)? //问号表示可能为空
opt_exponent = ('E'('+' + '-' + ε) digits) + ε
//('E'('+' + '-')? digits)?
num = digits opt_fraction opt_exponent
//opt_fraction == optional fraction(小数)
//opt_exponent == optional exponent(指数)
04-01: Lexical Specification
上节总结
At least one: A⁺ ≡ AA*
Union: A|B ≡ A + B
Option: A? ≡ A + ε
Range: 'a'+'b'+...+'z' ≡ [a-z]
Excluded range:
complement of [a-z] ≡ [^a-z]
为每个token class制定rexp
Number = digit⁺
Keyword = 'if' + 'else' + ...
Identifier = letter(letter + digit)*
OpenPar = '('
......
关于Lexical Specification
- 总是优先查找Maximal Munch(Match as long as possible)
=
==
- 总是选择优先度最高的(Highest priority match)
按照惯例,写Identifier时不能和keyword重名,所以通常将其解析为keyword。从另一个角度,如果遵循上述原则,keyword也是优先于identifier的。
if ∈ L(Keywords)
if ∈ L(Identifiers)
- 如果没有匹配的rexp,就写一个error rexp,包含error strings,并将其置于最底下(Put it last in priority)
Summary
-
Regular expressions provide a concise notation for string patterns
-
Use in lexical analysis requires small extensions
– To resolve ambiguities
– To handle errors
-
Good algorithms known
– Require only single pass over the input
– Few operations per character (table lookup)
04-02: Finite Automata Part 1
Regular expressions = specification
Finite automata = implementation
A finite automaton consists of
- An input alphabet Σ
- A set of states S
- A start state n
- A set of accepting states F ⊆ S
- A set of transitions state →(input) state
关于transition,从start state读取input然后转至另一个state,如果input结束(enter final state)并且进入accepting state就accept,否则就reject(S∉F or automata gets stuck)
视频中所举的三个例子,一是start state为A,accept state为1,input为1,state A通过transition至state B,然后input结束并accept;二是accept state为2,input为1但没有transition,所以get stuck然后reject结束;三是input为10 ,state A先读取input中的1通过transition进入state B,然后再读取input中的0,由于没有transition所以reject结束
Language of a FA ≡ set of accepted strings
例题:A finite automaton accepting any number of 1’s followed by a single 0 (Alphabet: {0,1})
input为110:start state为A,input pointer从input中的1开始,通过transition返回state A,然后读取1返回state A,读取0进入state B,input结束并进入accepting state,accept结束
input为100:start state为A,input pointer从input中的1开始,通过transition返回state A,然后读取0进入state B,再读取0,没有transition就会get stuck,reject结束
04-02: Finite Automata Part 2
Another kind of transition: ε-moves
Machine can move from state A to state B without reading input
Epsilon transition definition from wikipedia
An epsilon transition (also epsilon move or lambda transition) allows an automaton to change its state spontaneously(自发地), i.e. without consuming an input symbol. It may appear in almost all kinds of nondeterministic automaton in formal language theory, in particular:
- Nondeterministic Turing machine
- Nondeterministic pushdown automaton
- Nondeterministic finite automaton
Deterministic Finite Automata (DFA:确定有限状态机)
- Exactly one transition per input per state(针对唯一的input仅有唯一的transition)
- No ε-moves
Nondeterministic Finite Automata (NFA:不确定有限状态机)
- Can have zero, one, or multiple transitions for one input in a given state
- Can have ε-moves
A DFA can take only one path through the state graph per input
A NFA accepts if some choices lead to an accepting state
NFA当input结束进入final state时,如果accepting state存在于set of possible states中,就会accept
DFA快,NFA小,各具优势
04-03: Regular Expressions into NFAs
Lexical Specification -> Regular Expressions -> NFA -> DFA -> Table-driven Implementation of DFA
课后习题:
A、C因为1*处transition不足直接排除,B为正确答案,D错在接受input为1后通过epsilon move返回的是start state,这样在start state可以通过epsilon move进入state 0,与题意不符
04-04: NFA to DFA
Epsilon Closure
某个state的Epsilon Closure是当前state能通过epsilon move到达的所有state的set(包括自身)
Epsilon closure for a given state X is a set of states which can be reached from the states X with only (null) or E moves including the state X itself.
图文笔记
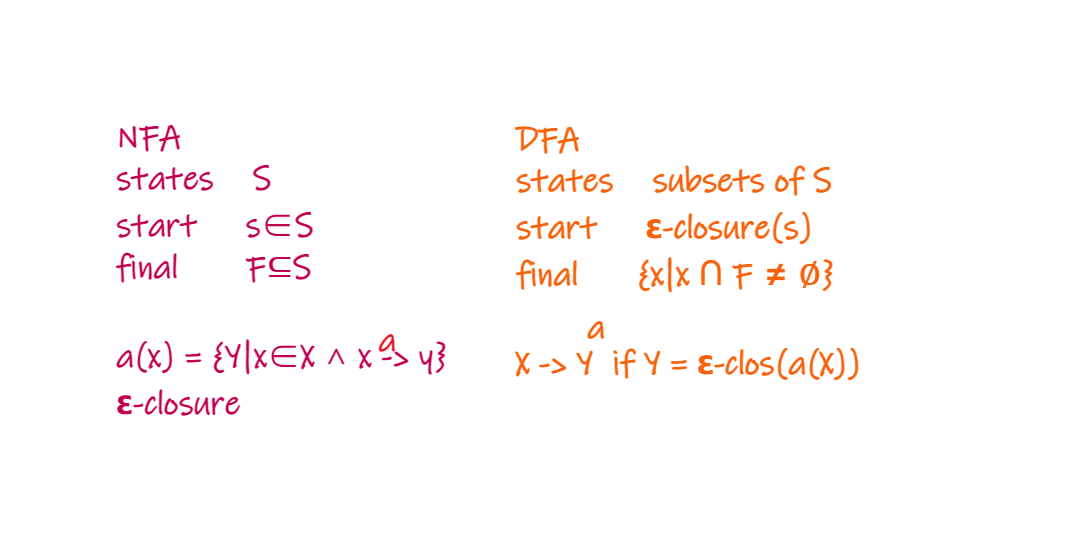
课后习题答案:D
首先写出start state(A)的Epsilon Closure,为ABCGHI,然后有两个transition
- input为1,进入state D,EC为DE,继续读取input 0,进入state F,EC为FGHBC,又重复读取input 1
- input为0,进入state J,EC为JH
直观图如下
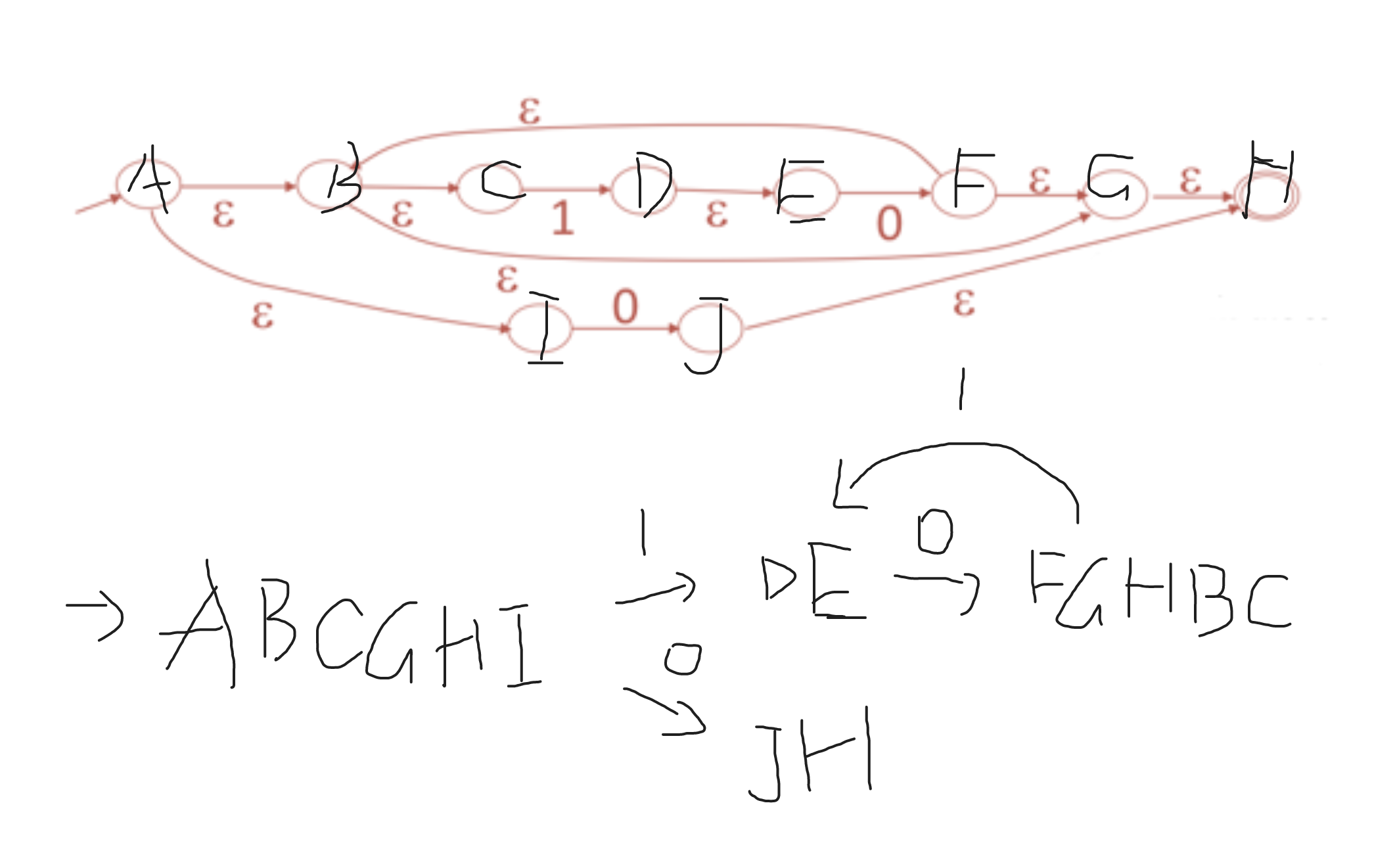
04-05: Implementing Finite Automata
A DFA can be implemented by a 2D table T
– One dimension is “states”
– Other dimension is “input symbol”
– For every transition Si →a Sk define T[i,a] = k
横坐标为input,纵坐标为state,表格中的值k为每个state在读取对应的input以后进入的next state
i = 0;
state = 0;
while(input[i]){
state = A[state,input[i++]];
}
如果重复的state过多,可以创建两个一维数组,对每个state用pointer指向对应input下的next state
NFA -> DFA conversion is key
Q.E.D.



